Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
Let's begin the Transum Newsletter for September 2023 with the puzzle of the month.
A dartboard breaks into two pieces. The sum of the numbers on one piece is twice the sum of the numbers on the other piece. Where was the break?
Don't forget Transum has a Digital Darts game you could play while thinking about the puzzle. Last week I added a button for subscribers to generate a link containing customised settings to send to pupils. Thanks to Lori for the suggestion.
Back to School did you say? Don't worry, I've got you covered. From equipment lists to introductory activities you will find many great ideas on the Back to School page.
Now what's new?
Number Stairs has been given a comple rewrite. It's a number investigation that requires the introduction of some algebra. There are many ways this investigation can be extended so it really is open-ended. The possibilities stretch to infinity and beyond (to quote a wooden actor!).
Where am I with Algebra? Maybe a tutor would use this with a new student to get a quick feel for how developed the student's knowledge of algbra is now and what might be the next step. I threw this together for a new student I was being introduced to so please let me know if you can suggest any improvements.
The Maths General Knowledge Quiz now has a Level 3. If Level 1 is for lower Secondary, Level 2 for upper Secondary then Level 3 (Containing questions such as "What is the smallest positive integer that is exactly divisible by all the numbers from 1 to 10?") is probably only for the 'outliers'!
Temperatures now has additional levels. The main focus is on working with negative numbers in context, though a link is provided to an additional exercise on converting between Fahrenheit and Celsius. Can you remember that formula?
Currency Converter: This is a minimalist currency conversion tool designed for quick results using only the major world currencies. Straight-forward and simple, no bells or whistles but I've already found it quite useful in 'real life'.
Thanks to Lauri Johnson for pointing out a possible ambiguity in the Rounding exercise. I have since added the following clarification to the Help tab, adapted from a Wikipedia article.
The significance of trailing zeros in a number not containing a decimal point can be ambiguous. For example, it may not always be clear if the number 1300 is precise to the nearest unit (just happens coincidentally to be an exact multiple of a hundred) or if it is only shown to the nearest hundreds due to rounding or uncertainty. The following widely recognised options are available for indicating the significance of number with trailing zeros:
For the purpose of answering the questions in the higher level exercises these methods are not necessary as your typed answers appear on the same page as the instructions stating the number of significant figures required.
How do they say the number 92 in some European countries?
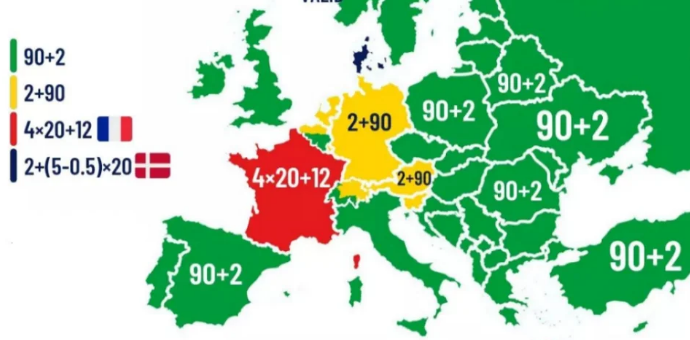
Map posted by u/Redstream28 in Reddit but original source unknown
There are no Transum subscribers in Denmark but if anyone from Denmark reads this newsletter and shares more information about 2+ (5-0.5) x 20 I'm sure we'd all be interested.
Talking about numbers (pun intended) how would you say 1500? Is it fifteen hundred or one thousand five hundred? Are both methods equally valid or do you have a preference?
Saying numbers out loud is the theme of the 19th September Lesson Starter. That date is also "Talk Like A Pirate Day" so I couldn't resist the temptation to combine these ideas. The numbers begin small so don't get lulled into a false sense of security - they start doubling and very soon you'll find yourself out of your depth (after walking the plank!).
Finally the answer to last month's puzzle which was: The average (mean) age of the four Calamity cousins is 20. The average (mean) age of the two youngest cousins is 14. The average (mean) age of the two cousins who each have both younger and older cousins is 18. The second youngest is half the age of the oldest. What is the range of their ages?
Answer: their ages are 12,16,20,32 so the range is 20.
The first five people to send in a correct answer were Mala Bhaduri, Chris Smith, Richard Bell, Allan Christie and Wil Ransome.
I'll share Richard's working:
Let the 4 cousins be C1, C2, C3 & C4 respectively.
C3 + C4 = 2 x 14 = 28
C2 + C3 = 2 x 18 = 36
C1 = 4 x 20 - (C2 + C3 + C4)
= 80 - (C2 + 28)
= 52 - C2
C1 = 2C3
so 2C3 = 52 - C2
so C3 = 52 - (C2 + C3)
= 52 - 36
Hence C3 = 16 and C1 = 2 x 16 = 32
C1 = 52 - C2
Therefore 32 = 52 - C2 and so C2 = 20.
C4 = 80 - (C1 + C2 + C3)
= 80 - (32 + 20 + 16)
= 80 - 68
So C4 = 12.
Therefore the range C1 - C4 = 32 - 12 = 20.
Check: C1 + C2 + C3 + C4 = 32 + 20 + 16 + 12 = 80
and 80/4 = 20, which is the mean age of the cousins.
That's all for now,
John
P.S. Today is the origin for the rest of your life. Adopt a negative squared attitude!
Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
