Newsletter

New Year Fence Painting

Thursday 1st January 2026

Happy New Year! This is the Transum Newsletter for the month of January, the first of 2026. It begins, as usual, with the puzzle of the month.

My New Year’s resolution is to paint the long fence that goes all the way around Tran Towers. In January I will paint 1/12 of the fence. In February I’ll paint 2/12 of the length of fence remaining. In March I’ll paint 3/12 of the remaining portion of the fence and so on throughout the year. When during the year will I require the most paint?

(Extension for rocket scientists: what if there were x months in a year instead of 12?)

If you get an answer, I'd love to hear how you solved the puzzle (or your students solved it). Fire off an email to: gro.musnarT@rettelsweN

While you think about that, here are some of the key resources added to the Transum website during the last month.

Jack Frost Fractions is a new interactive activity in which students frost the panes of a window to satisfy a set of fraction clues. They work with fractions of a whole grid and of different regions (top section, left section, particular rows), and must use logical reasoning to find a pattern that fits all the conditions rather than just carrying out routine calculations. I developed this in mid-December as a late addition to the Christmaths collection, but as it has more of a general winter theme I have chosen to introduce it in this January newsletter.

Moon Measures is a practical estimating activity that can lead to some rich follow-up work. As students work through the questions, a results table is built up showing their estimates, percentage errors, time taken and running score. If they copy and paste this table into a spreadsheet, it opens the door to a great deal of meaningful mathematics: calculating averages, comparing performance on different scales, creating graphs of error against distance or time, and discussing what "good" estimation looks like.

A new year is the perfect time to raise the subject of Time in your maths lessons. I am always surprised by the students who can use the formula to solve quadratic equations but don't know the number of days in the Months of the Year.

You could start with the 1st January Starter, which includes some time calculations. You may want to show the video I have just added about the etymology of time words. And just for the student who thinks they know it all, ask them the meaning of "bimonthly". Does it mean occurring twice in a month or once every two months? My dictionary says it can mean both, so perhaps a survey is called for!

Forthcoming January dates to mention in Maths lessons:

4 January :: World Trivia Day

29 January :: Chinese New Year

29 January :: International Puzzle Day

Don't forget you can listen to this month's podcast, which is the audio version of this newsletter. You can find it here, on Spotify or on Apple Podcasts. You can follow Transum on Bluesky, Twitter (some call it X) and 'like' Transum on Facebook.

I've had a steady stream of comments over the years suggesting that the Rotational Symmetry activities should refer to order of symmetry one instead of none. Here's what I'm thinking:

What reputable sources say

• The NCETM glossary states that a 2-D shape has rotational symmetry about a point if it matches itself after a rotation through some angle greater than 0° and less than 360°. It defines the order as the number of distinct matches in a full turn. Saying "order 1" is technically true because every shape matches after 360°, although this is not very informative.
• GCSE revision materials commonly avoid "order 0". They either write "no rotational symmetry" or accept "order 1" for the trivial full-turn only case.
• Many teachers prefer to say "no rotational symmetry" to avoid confusion.

My preference for secondary teaching

1. Teach the NCETM definition that requires an angle strictly between 0° and 360° for a match.
2. When a shape only matches after a full turn, write no rotational symmetry.
3. If an exam board allows "order 1", mention it in your exam preparation, yet reserve "order n" for n ≥ 2 in everyday teaching.
4. For irregular shapes like the one below, describe them as asymmetric with no rotational symmetry.

The Mathemagic page contains many tricks that a teacher can demonstrate to pupils and one of my favourites is the Magic Square trick. I remember showing it to my classes many years ago when I was trying to show off the magical powers that all Maths teachers have! So a couple of weeks ago I was amazed to see another Magic Square trick on a YouTube video that used a totally different method based on binary numbers.

The trick featured in the video is John Walton’s Magic Square, also known as "Da Vinci Outnumbered". 

The entire trick is based on 16 double-sided cards arranged in a 4x4 grid, allowing the magician to adjust the total on the fly based on the number the audience creates.

The 16 cards are pre-assigned into four distinct groups. These groups allow the magician to adjust the final total of the magic square by any value from 1 to 15 (or from 3 to 18 as the sum of three dice):

• Group 1: Cards in this group have a difference of 1 between the front and back sides.
• Group 2: Cards in this group have a difference of 2.
• Group 3: Cards in this group have a difference of 4.
• Group 4: Cards in this group have a difference of 8.

By combining these differences, the magician can create any adjustment value needed (e.g., to increase the total by 7, he flips Group 1 + Group 2 + Group 4 cards, since 1 + 2 + 4 = 7).

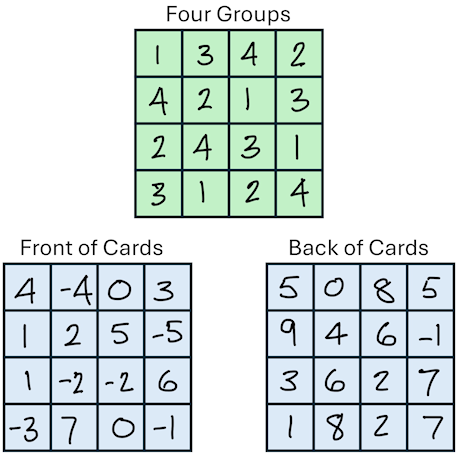
I'm not sure if my interpretation of the method exactly matches John Walton's, but here is how it is performed:

1. The audience members (Penn, Teller, and Alyson) are asked to mentally roll a die and call out the results (e.g., 3, 1, 4), which are summed to create the final target number (e.g., 8).
2. The cards are pre-set to total a specific "base number" (I guess that's 3), in all directions (rows, columns, diagonals, centre).
   • The magician quickly calculates the difference between the base number and the audience's target number (8 - 3 = 5).
   • He uses the binary system (1, 2, 4, 8) to determine which cards must be flipped to achieve that difference. So, for 5 he would need to flip the cards in Group 1 (adding 1) and Group 3 (adding 4).
   • The cards are laid out in a special pattern where the groups are positioned so that flipping the same groups in every column automatically ensures that every row, column, and diagonal adds up to the new target number.

The secret described in the video is a complex yet elegant application of Maths and misdirection that earned John Walton a "Fool Us" trophy.

Finally the answer to last month's puzzle which was:

Two elves, Holly and Mistle, are helping to fill a magical toy sack for Santa. Working together, they can fill the sack in 22.5 minutes. The quicker elf could fill the sack all by their 'self', 24 minutes faster than the slower elf.

How many minutes would it take each elf to fill the toy sack on their own?

The answers are 36 minutes and 60 minutes.

Thanks to all those who sent in solutions, and I've included some of the methods below.

That's all for now,

John

P.S. When looking back six years ago with hindsight, we can say we have 2020 vision!

Home :: Previous Newsletters :: Podcast

Do you have any comments? It is always useful to receive feedback on this newsletter and the resources on this website so that they can be made even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.

Did you know you can follow this newsletter on Substack completely free of charge? Please note this is separate from a paid subscription to the Transum website, which unlocks a much wider range of premium resources.