
 |
Exam-Style Question on KinematicsA mathematics exam-style question with a worked solution that can be revealed gradually |
Question id: 616. This question is similar to one that appeared on an IB AA Standard paper in 2021. The use of a calculator is allowed.
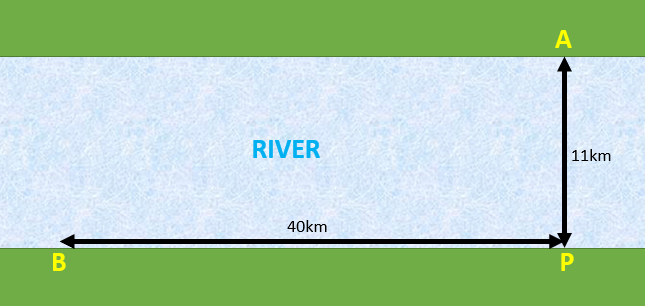
The widest river in the world has a width of 11km at its widest point. Suppose there were a straight length of this river near Awkwardville (A) as shown in the diagram below. Points A and P lie on opposite banks, such that AP is the shortest distance across the river. Point B represents the centre of Bumblingburg which is located on the southern riverbank.
$$PB = 40km, AP = 11km \text{ and angle } A \hat{P}B = 90° $$A boat travels at an average speed of \(12km h^{-1}\).
A bus travels along the straight road
between P and B at an average speed of \(30kmh^{-1}\).
(a) Find the travel time, in hours, from A to B given that the boat is taken from A to P, and the bus from P to B.
(b) Find the travel time, in hours, from A to B given the boat travels directly to B.
There is a point D which lies on the road from P to B. such that \(BD = x km\).
(c) If the boat travels from A to D and the bus travels from D to B, find an expression, in terms of \(x\), for the travel time T, from A to B, passing through D.
(d) Find the value of \(x\) so that T is a minimum.
An excursion involves renting the boat and the bus. The cost to rent the boat is £50 per hour and the cost to rent the bus is £35 per hour.
(e) Find the new value of \(x\) so that the total cost to travel from A to B via D is a minimum.
(f) Write down the minimum total cost for this journey.
|
The worked solutions to these exam-style questions are only available to those who have a Transum Subscription. Subscribers can drag down the panel to reveal the solution line by line. This is a very helpful strategy for the student who does not know how to do the question but given a clue, a peep at the beginnings of a method, they may be able to make progress themselves. This could be a great resource for a teacher using a projector or for a parent helping their child work through the solution to this question. The worked solutions also contain screen shots (where needed) of the step by step calculator procedures. A subscription also opens up the answers to all of the other online exercises, puzzles and lesson starters on Transum Mathematics and provides an ad-free browsing experience. |
|

Drag this panel down to reveal the solution
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.
Do you have any comments about these exam-style questions? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
©1997 - 2026 Transum Mathematics :: For more exam-style questions and worked solutions go to Transum.org/Maths/Exam/