Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Probability Video A reminder of how to work out basic probability leading to simple combined events and expected values.
Probability Video A reminder of how to work out basic probability leading to simple combined events and expected values. Probability Basic probability questions in an online exercise.
Probability Basic probability questions in an online exercise.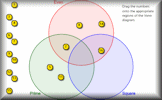 Venn Diagram Place each of the numbers 1 to 16 on the correct regions on the Venn diagram.
Venn Diagram Place each of the numbers 1 to 16 on the correct regions on the Venn diagram. Snail Race Projectable Twelve snails have a race based on the sum of two dice. This is the teachers' version of the race simulation.
Snail Race Projectable Twelve snails have a race based on the sum of two dice. This is the teachers' version of the race simulation.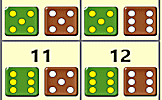 Two Dice Possibility Space An interactive visual aid showing the possibility space obtained when throwing two dice
Two Dice Possibility Space An interactive visual aid showing the possibility space obtained when throwing two dice Snail Race A race between 12 snails. Which snail is most likely to win? This is the students' version of the race simulation.
Snail Race A race between 12 snails. Which snail is most likely to win? This is the students' version of the race simulation.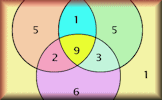 Venn Totals Practise reading and creating Venn diagrams containing two and three sets and the number of elements in those sets.
Venn Totals Practise reading and creating Venn diagrams containing two and three sets and the number of elements in those sets. Venn Paint Video Here is a demonstration of how to illustrate union, intersection and complement of sets as they appear in Venn diagrams.
Venn Paint Video Here is a demonstration of how to illustrate union, intersection and complement of sets as they appear in Venn diagrams.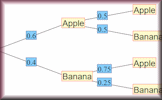 Tree Diagram Creator Quickly create a probability tree diagram to use as a visual aid.
Tree Diagram Creator Quickly create a probability tree diagram to use as a visual aid.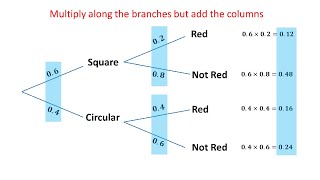 Tree Diagrams Video Tree diagrams can be really helpful showing combinations of two or more events in order to calculate probabilities.
Tree Diagrams Video Tree diagrams can be really helpful showing combinations of two or more events in order to calculate probabilities.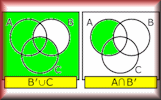 Venn Paint Flood fill the regions of the Venn diagrams according to the given statements.
Venn Paint Flood fill the regions of the Venn diagrams according to the given statements. Tree Diagrams Calculate the probability of independent and dependent combined events using tree diagrams.
Tree Diagrams Calculate the probability of independent and dependent combined events using tree diagrams. Venn Matching Game Match the sets statement with the equivalent Venn diagram. A drag and drop self marking exercise.
Venn Matching Game Match the sets statement with the equivalent Venn diagram. A drag and drop self marking exercise. Venn Diagram Pairs The traditional pairs or pelmanism game adapted to test knowledge of Venn diagrams.
Venn Diagram Pairs The traditional pairs or pelmanism game adapted to test knowledge of Venn diagrams.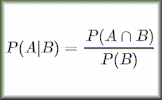 Conditional Probability Find the probability of one event happening given that another event has already happened.
Conditional Probability Find the probability of one event happening given that another event has already happened.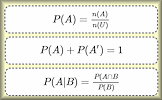 Probability Formulae Show that you know which formula (as given in the IB Formula Booklet) to use for each probability question. A drag and drop challenge.
Probability Formulae Show that you know which formula (as given in the IB Formula Booklet) to use for each probability question. A drag and drop challenge.
Here are some exam-style questions on this statement:
- "If the universal set is the set of positive even numbers less than 30 and:" ... more
- "(a) Complete the Venn diagram with the following information." ... more
- "(a) Complete the Venn diagram to represent this information:" ... more
- "The midnight train to Georgia is not the most reliable. The probability that the train will be late on any day is 0.35" ... more
- "Near Blizzard Lodge on any day the probability that it snows is \( \frac{1}{4} \)." ... more
- "(a) There are 24 people at a Football Club supporters' meeting in Dudley. Thirteen of them are female." ... more
- "Mrs Gill wants to give her nephew two sweets from a jar she keeps on her kitchen table. There are 11 sweets in this jar." ... more
- "A driving test has two sections, practical(p) and theory(t). One day everyone who took the test passed at least one section. 77% passed the practical section and 81% passed the theory section." ... more
- "The Venn diagram represents a collection of 40 books on sale in an online store." ... more
- "A box contains only green and yellow crayons." ... more
- "At an international conference there were 300 delegates from both the northern and southern hemispheres. Each delegate wore a t-shirt in one of three different colours:" ... more
- "Lisa's nephew Sean has two boxes containing plastic building bricks." ... more
- "(a) Use set notation to describe the shaded region in the Venn diagram on the left." ... more
- "80 students are asked if they like History (\(H\)) and if they like Geography (\(G\))." ... more
- "Twenty nine children went to a zoo to photograph some animals. The numbers of children who photographed Lions(L), Monkeys(M) and Zebras (Z) are given as follows:" ... more
- "Neal is attending a Scout jamboree in Japan. He has both boots and trainers to wear. He also has the choice of wearing a cap or not." ... more
- "Let \(J\) and \(T\) be independent events, where \(P(J)=0.4\) and \(P(T)=0.7\)." ... more
- "On the day after one GCSE paper Twitter and the media were buzzing with comments about a particular question about Hannah's sweets. Here is the Transum version of this now famous Maths exam question:" ... more
- "When the arrow is spun once on this spinner, a 1 or a 2 or a 3 can be scored depending on the colour the arrow lands on." ... more
- "Let A and B be events such that \(P (A) = 0.45\) , \(P (B) = 0.35\) and \(P (A \cup B) = 0.5\)." ... more
- "Bag A contains 6 green tickets and 5 blue tickets." ... more
- "Sumville has three newspapers: The Chronicle, The Express and Moon, and The Scribe." ... more
- "The Venn diagram below shows the events \(A\) and \(B\), and the probabilities p, q and r." ... more
- "Events \(A\) and \(B\) are such that \(P(A) = 0.25\), \(P(A|B) = 0.15\) and \(P(A \cup B) = 0.65\)." ... more
- "900 professional footballers were surveyed with the following results" ... more
- "Julie chooses a cake from a yellow box on a shelf. The box contains two chocolate cakes and three plain cakes. She eats the cake and chooses another one from the box. The tree diagram below represents the situation with the four possible outcomes where C stands for chocolate cake and P for plain cake." ... more
- "Jane and David play two games of golf. The probability that Jane wins the first game is \(\frac56\). If Jane wins the first game, the probability that she wins the second game is \(\frac67\)." ... more
- "At a fitness club, \( 60\% \) of the members are full-time members, and \( 30\% \) of the members participate in group fitness classes. \( 25\% \) of the members are neither full-time members nor participate in group fitness classes." ... more
- "Mathsland's national currency comes in denominations of 1 unit, 5 units, 10 units and 50 units. Sofya places this collection of these coins in her purse then, without looking, takes out two coins at random, one after the other." ... more
- "Two events A and B are such that \(P(A) = 0.57\) and \(P (A \cap B) = 0.21\)." ... more
- "Some orange fish and green fish are swimming in a large tank in the enterance to a restaurant. The number of orange fish is a single digit number as is the number of green fish." ... more
Here are some Advanced Starters on this statement:
- Bertrand's Box Paradox
Bertrand's box paradox is a paradox of elementary probability theory, first posed by Joseph Bertrand in 1889 more - Best Dice
Which of the unusual dice would you choose to give you the best chance of winning the prize? more - Other Child's Gender
What is the probability that the other child is also a boy? more - Perennial Rivals
Which football team will be first to win four games? more - Singers and Dancers
What fraction of the singers and dancers are both singers and dancers? more - Sorcerer's Apprentices
The difference between random selection and an 'at least' scenario involving sorcerer's apprentices. more - Tri-Junction
A real life situation that can be analysed with the use of a tree diagram. more - Two Pots
Use tree diagrams to find the surprising result that probabilities of different situations are the same. more - Unfinished Game
Share the prize in a fair ratio according to the probability of each player winning. more - What Question?
Write down all the possible questions that could have been asked if this was the Venn diagram provided in a mathematics exam. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
This Bicen Maths video clip shows everything you need to memorise on probability for A Level Statistics.
This video on Conditional Probability is from Revision Village and is aimed at students taking the IB Maths AA SL/HL level course.
In the study of probability, various visual tools and formulae are employed to simplify and understand complex events. One such tool is the Venn diagram, which visually represents the relationship between different sets. Similarly, tree diagrams depict sequential events, while sample space diagrams and tables of outcomes provide a comprehensive view of all possible outcomes of a random experiment.
When dealing with combined events, the probability of either event A or event B occurring is given by \( P(A \cup B) \). This is calculated as the sum of the probabilities of each event minus the probability of both events occurring simultaneously. On the other hand, if two events are mutually exclusive, meaning they cannot occur at the same time, their intersection probability \( P(A \cap B) \) is zero.
Conditional probability, denoted as \( P(A|B) \), represents the probability of event A occurring given that event B has already occurred. Lastly, if two events are independent, the occurrence of one does not affect the occurrence of the other, and their intersection probability is the product of their individual probabilities.
Here are the key formulae:
$$ P(A \cup B) = P(A) + P(B) - P(A \cap B) \\ P(A \cap B) = 0 \quad \text{(For mutually exclusive events)} \\ P(A|B) = \frac{P(A \cap B)}{P(B)} \\ P(A \cap B) = P(A)P(B) \quad \text{(For independent events)} $$Let's consider an example to illustrate these concepts:
Suppose we have two events: A, which represents drawing a red card from a standard deck of cards, and B, which represents drawing a face card (Jack, Queen, or King). The probability of drawing a red card, \( P(A) \), is \(\frac{26}{52}\) or \(\frac{1}{2}\). The probability of drawing a face card, \( P(B) \), is \(\frac{12}{52}\) or \(\frac{3}{13}\). The probability of drawing a red face card (intersection of A and B), \( P(A \cap B) \), is \(\frac{6}{52}\) or \(\frac{3}{26}\). Using the formula for combined events:
$$ P(A \cup B) = P(A) + P(B) - P(A \cap B) \\ P(A \cup B) = \frac{1}{2} + \frac{3}{13} - \frac{3}{26} = \frac{16}{26} \text{ or } \frac{8}{13} $$Thus, the probability of drawing either a red card or a face card from a standard deck is \(\frac{8}{13}\).

Transum,
Saturday, August 17, 2019
"An Advanced Starter that can be investigated by constructing sample spaces (or possibility spaces) is Best Dice.
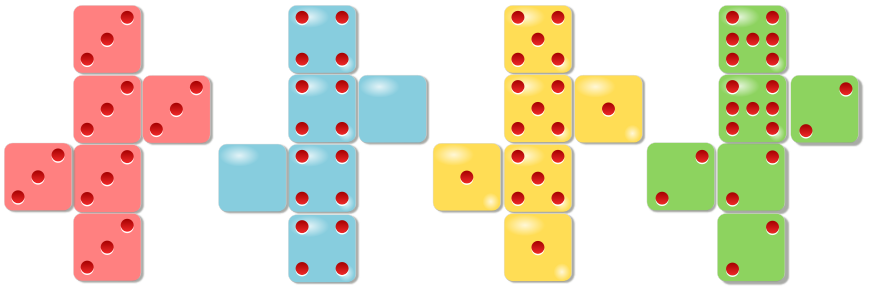 "
"
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

