Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
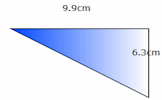 Pythagoras Basics A drill and practice self marking exercise on the basics of Pythagoras' theorem.
Pythagoras Basics A drill and practice self marking exercise on the basics of Pythagoras' theorem.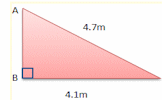 Pythagoras An online exercise to test your understanding of and ability to apply Pythagoras' Theorem.
Pythagoras An online exercise to test your understanding of and ability to apply Pythagoras' Theorem. Demonstrating Pythagoras Short clip from QI: Stephen Fry demonstrates Pythagoras' theorem.
Demonstrating Pythagoras Short clip from QI: Stephen Fry demonstrates Pythagoras' theorem.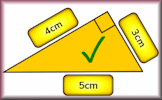 Make Them Right Arrange the measurements next to the sides of the triangles so that each diagram is correct according to Pythagoras' Theorem.
Make Them Right Arrange the measurements next to the sides of the triangles so that each diagram is correct according to Pythagoras' Theorem. Pythagoras' Theorem Video The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.
Pythagoras' Theorem Video The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.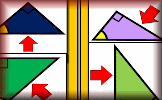 Which Side? Arrange the diagrams in groups depending on whether the arrow is pointing to the opposite, adjacent or hypotenuse.
Which Side? Arrange the diagrams in groups depending on whether the arrow is pointing to the opposite, adjacent or hypotenuse. Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles.
Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles. Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles.
Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles. Trig-Pythag Fusion Problems requiring multi-step solutions using both Trigonometry and Pythagoras' Theorem
Trig-Pythag Fusion Problems requiring multi-step solutions using both Trigonometry and Pythagoras' Theorem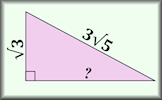 Pythagoras with Surds Questions about right-angled triangles for which the answers should be surds in their simplest form.
Pythagoras with Surds Questions about right-angled triangles for which the answers should be surds in their simplest form.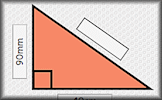 Pythagorean Probe Use Pythagoras' Theorem to help find all of the measurements of these right angles triangles.
Pythagorean Probe Use Pythagoras' Theorem to help find all of the measurements of these right angles triangles.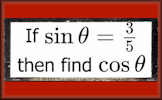 If Then Trigonometry Finding the exact values of sine, cosine and tangent of angles if given a different trig ratio.
If Then Trigonometry Finding the exact values of sine, cosine and tangent of angles if given a different trig ratio.
Here are some exam-style questions on this statement:
- "\(ABC\) is a right-angled triangle." ... more
- "An isosceles triangle shaped frame is made from four pieces of metal. The frame has a height of 8 metres and a base of length 12 metres." ... more
- "Work out the value of \(x\), the length in centimetres of one of the sides of this right-angled triangle." ... more
- "ABC is a right-angled triangle as shown in the diagram below. Calculate the length of AB giving your answer correct to three significant figures." ... more
- "An arborist sights the top of a tree using a clinometer and reads the angle of elevation to be 29o. Her clinometer is 28 metres from the base of the tree and is on a tripod making it 1.5 metres above ground level." ... more
- "The diagram shows a right-angled triangle and a semicircle. The straight side of the semicircle is the same length as the longest side of the triangle." ... more
- "The diagram shows a trapezium where the sides AC and BD are parallel." ... more
- "Four copies of a green right-angled triangle are used to enclose a yellow square." ... more
- "The diagram shows a quadrilateral, ABCD, formed from two triangles, ABC and ACD." ... more
- "A triangular prism is made using two right-angled triangles and three rectangular pieces of cardboard. Five of the vertices have been labeled \(A, B, C, D \text{ and } E\) as shown in the photograph below." ... more
- "The diagram shows a rectangular-based pyramid, TABCD (not drawn to scale)." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Pythagoras Pythagoras was a Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. He is most famous for his theorem connecting the lengths of the sides of right angled triangles. His theorem states that the squares of the lengths of the two shorter sides of any right-angled triangle will add up to the square of the length of the longest side (the hypotenuse). This theorem can be used to calculate the length of any side of a right-angled triangle if the lengths of the other two sides are known. Do you know when the next Pythagorean Day is? It will occur when the square of the day added to the square of the month equals the square of the last two digits of the year.
- Trigonometry Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Pupils begin by learning the names on the sides of a right-angled triangle relative to the angles. They then learn the ratios of the lengths of these sides and the connection these ratios have with the size of the angles. Having mastered right-angled triangle trigonometry pupils then progress to more advanced uses including the sine rule and cosine rules. The use of a scientific or graphing calculator is essential for this topic and correct, efficient use of the calculator is an important skill to develop. Here's a Trigonometry Wordsearch just for fun.
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

