Refreshing Revision

Number Sequences 1

What is the 6th:
a) Odd number; 11
b) Square number; 36
c) Prime number. 13

Factors

Find all the factors of:

20

1, 2, 4, 5, 10, 20.

Multiples

Subtract the 5th from the 8th multiples of:

12

36

Polygons

What are the names of regular polygons with:
a) six sides;
b) seven sides;
c) eight sides.

Hexagon, Heptagon and Octagon (all regular)

Rounding (3sf)

Round to three significant figures:
a) 50.25; 50.3
b) 438115; 438000
c) 52; 52.0
d) 0.005295; 0.00530

Area of a Triangle

Find the area of a triangle that has a base of 5cm and a height of 10cm.

25cm²

Area of a Trapezium

Find the area of a trapezium that has a base of 9cm, a height of 10cm and a top (parallel to base) of 3cm. 60cm²

Fractions (Adding)

Evaluate:

$ \frac{3}{5} + \frac{8}{10}$ $= 1\frac{2}{5}$

Fractions (Multiplying)

Evaluate:

$ \frac{1}{2} × \frac{3}{4}$ $= \frac{3}{8}$

Fractions (Dividing)

Evaluate:

$ \frac{2}{4} ÷ \frac{7}{6}$ $= \frac{3}{7}$

Circle (Vocabulary)

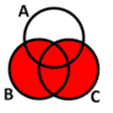
Name the red part.

Venn Diagrams

Describe the red region.

Shape Formulas

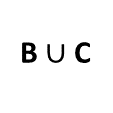
What is the formula?

Formulas (Advanced)

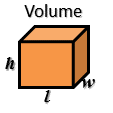
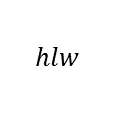
What is it?

Fraction to Percentage

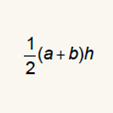
Convert this fraction to a percentage to 3 significant figures.

$ \frac{5}{9}$ $= 55.6$%

Circle Area

Find the area of a circle that has a radius of 10cm. Give your answer to three significant figures.

314cm²

Circle Circumference

Find the circumference of a circle that has a radius of 10cm. Give your answer to three significant figures.

62.8cm

Decimals (Adding)

Calculate the value of:

9.8 + 6.5

= 16.3

Decimals (Subtracting)

Calculate the value of:

6.2 − 3.9

= 2.3

Decimals (Multiplying)

Calculate the value of:

4.5 × 7.8

= 35.1

Decimals (Dividing)

Calculate the value of:

76.7 ÷ 13

= 5.9

Indices (Simple)

What is the value of:

2³

= 8

Indices (Advanced)

What is the value of:

$4^{-3}$

$= \frac{1}{64}$

Basic Addition

Calculate the value of:

56 + 75

= 131

Basic Subtraction

Calculate the value of:

83 − 26

= 57

Basic Multiplication

Calculate the value of:

64 × 92

= 5888

Basic Division 2

Calculate the value of:

1653 ÷ 29

= 57

Percentage (Of)

Find the value of:

35% of 380

= 133

Standard Form 1

Find the value of:

6.3 × 10⁴

= 63000

Highest Common Factor

Find the highest common factor of forty five and twenty.

= 5

Times Tables (2-5)

4 × 2 = 8	3 × 2 = 6
5 × 5 = 25	6 × 2 = 12
7 × 5 = 35	8 × 5 = 40
9 × 5 = 45	2 × 4 = 8

Times Tables (2-12)

3 × 12 = 36	6 × 10 = 60
8 × 10 = 80	5 × 5 = 25
4 × 11 = 44	9 × 6 = 54
7 × 4 = 28	2 × 4 = 8

Times Tables (2)

9 × 2 = 18	3 × 2 = 6
4 × 2 = 8	6 × 2 = 12
7 × 2 = 14	8 × 2 = 16
5 × 2 = 10	2 × 2 = 4

Times Tables (3)

7 × 3 = 21	9 × 3 = 27
3 × 3 = 9	8 × 3 = 24
5 × 3 = 15	6 × 3 = 18
4 × 3 = 12	2 × 3 = 6

Times Tables (4)

9 × 4 = 36	3 × 4 = 12
5 × 4 = 20	8 × 4 = 32
6 × 4 = 24	4 × 4 = 16
7 × 4 = 28	2 × 4 = 8

Times Tables (5)

8 × 5 = 40	6 × 5 = 30
4 × 5 = 20	9 × 5 = 45
5 × 5 = 25	7 × 5 = 35
3 × 5 = 15	2 × 5 = 10

Times Tables (6)

4 × 6 = 24	6 × 6 = 36
9 × 6 = 54	3 × 6 = 18
8 × 6 = 48	5 × 6 = 30
7 × 6 = 42	2 × 6 = 12

Times Tables (7)

8 × 7 = 56	5 × 7 = 35
9 × 7 = 63	3 × 7 = 21
6 × 7 = 42	4 × 7 = 28
7 × 7 = 49	2 × 7 = 14

Times Tables (8)

8 × 8 = 64	5 × 8 = 40
9 × 8 = 72	7 × 8 = 56
6 × 8 = 48	4 × 8 = 32
3 × 8 = 24	2 × 8 = 16

Times Tables (9)

7 × 9 = 63	3 × 9 = 27
8 × 9 = 72	6 × 9 = 54
5 × 9 = 45	9 × 9 = 81
4 × 9 = 36	2 × 9 = 18

Times Tables (12)

5 × 12 = 60	3 × 12 = 36
4 × 12 = 48	7 × 12 = 84
9 × 12 = 108	8 × 12 = 96
6 × 12 = 72	2 × 12 = 24

Fractions (Equivalent)

Write this fraction in its simplest form:

$ \frac{20}{24}$ $= \frac{5}{6}$

Fractions (Mixed)

Evaluate:

$ 3\frac{2}{3} − \frac{5}{6}$ $= 2\frac{5}{6}$

Pythagoras

Find AC if AB = 3.3m and BC = 5m. 3.76m

Trigonometry (Angle)

Find angle BCA if AB = 3.1m and BC = 4.3m. 46.1^o

Trigonometry (Side)

Find BC if angle BCA = 45^o and AB = 4.6m. 6.51m

Roman Numerals (1-12)

Give your answer in Roman numerals.

²

Roman Numerals (60-100)

Give your answer in Roman numerals.

²

Roman Numerals (Large)

Give your answer in Roman numerals.

²

Fraction to Decimal

Convert this fraction to a decimal.

$ \frac{3}{5}$ $= 0.6$

Decimal to Fraction

Convert this decimal to a fraction.

$0.48$ = $ \frac{12}{25}$

Percentage (Increase)

Increase £160 by 45%

£232

Lowest Common Multiple

What is the lowest common multiple of six and fifteen.

= 30

Sequence (Arithmetic)

4,13,22,31,40...

Find the:
a) next term; 49
b) n^th term; 9n - 5
c) term number 35; 310

Sequence (Geometric)

6,18,54,162,486...

Find the:
a) next term; 1458
b) n^th term; 6 × 3^n-1
c) term number 10; 118098

Interest (Simple)

If £120 is invested for 5 years with a simple interest rate of 5%, find the amount of interest earned. £30.00

Interest (Compound)

If £240 is invested with an interest rate of 4% compounded annually, find the value of the investment after 7 years. £315.82

Currency Exchange

If £1 is worth $1.28, convert:

a) £200 to dollars; $256.00

b) $180 to pounds; £140.63

Coordinates (Midpoint)

What are the coordinates of the midpoint of the line joining:

$(7,6) \text{ and } (19,16)$

(13,11)

Gradient

What is the gradient of the line joining:

$(5,-2) \text{ and } (11,4)$

1

Coordinates (Square)

Here are the coordinates of 3 vertices of a square, what are the coordinates of the 4^th?

$(1,5),(6,8),(-2,10)$

(3,13)

Negative Numbers

a) 6 − 12 = -6
b) 6 × (-8) = -48
c) (8−16)(8−19) = 88
d) 48 ÷ (-8) = -6
e) (-10)² = 100

Substitution

If p = 5, q = 17 and
r = -11 evaluate:

a) 2q − p = 29
b) pq + r = 74
c) p² − 5q - r = -49

Equations (Type 1)

Solve:

$3x = 21$

$x = 7$

Equations (Type 2)

Solve:

$5x +9= 34$

$x = 5$

Equations (Type 3)

Solve:

$7x +6= 2x + 36$

$x = 6$

Equations (Type 4)

Solve:

$3(2x +5)-8= 55$

$x = 8$

Equations (Type 5)

Solve:

$4(4x + 2)= 3(4x + 5)$

$x = 1.75$

Equations (Simultaneous 1)

Solve:

$4x-2y = -6$
$3x-2y = -8$

$x = 2, y = 7$

Equations (Simultaneous 2)

Solve:

$4x+4y = 32$
$5x+8y = 46$

$x = 6, y = 2$

Equations (Simultaneous 3)

Solve:

$2x+2y = -35$
$3x-5y = 19.5$

$x = -8.5, y = -9$

Sets (Union)

Find the union of:

{6,7,8,9,10} and
{1,3,6,10,15}

{1,3,6,7,8,9,10,15}

Sets (Intersection)

Find the intersection of:

{5,6,7,8,9,10} and
{3,4,5,6,7,8}

{5,6,7,8}

Bearings

A plane flies from point A to point B on a bearing of 170^o. What bearing would it return on from B to A? 350^o

Probability

A number is picked at random from the set

{2,6,12}

what is the probability it is even? 1

BIDMAS

Evaluate:

6² − 9 × 9 + 4

-41

Simplify

Simplify the following by collecting like terms:

$6m+7+5m+8$

$11m+15$

Ratio

Divide 126 in the ratio

5:4

70 and 56

Graph Linear (1)

Draw a rough sketch of the graph of:

$2y=x-4$

Gradient 0.5
y intercept -2

Prime Factors

Express the following number as the product of prime numbers:

30

2 x 3 x 5

Percentage (Reverse)

In a sale an item costs £78 after a 35% reduction. What was the original price?

£120

Averages

Find the mean, mode, median and range of the following:

6,7,8,9,10

Mean = 8, no mode,
median = 8 and range = 4

Time (Analogue)

What time is this?

Time (Digital)

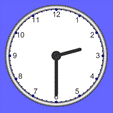
Sketch a clock face:

Decimals (Recurring)

Write the following recurring decimal as a fraction in its lowest terms.

0.828282... $\frac{82}{99}$

Percentage (Decrease)

Decrease £20 by 25%

£15

Brackets (Linear)

Expand:

$4(2x-6)$

$8x-24$

Brackets (Quadratic)

Expand:

$(3x+2)(4x-4)$

$12x^2-4x-8$

Factorise (Linear)

Factorise:

$12x-9$

$3(4x-3)$

Factorise (Quadratic 1)

Factorise:

$x^2-4$

$(x+2)(x-2)$

Factorise (Quadratic 2)

Factorise:

$5x^2+16x-16$

$(x+4)(5x-4)$

Circle Theorems

Which theorem?

Standard Form 2

Find the value of:

8.27 × 10^-4

= 0.000827

Standard Form 3

Write in standard form:

273000

= 2.73 × 10⁵

Standard Form 4

Write in standard form:

0.0604

= 6.04 × 10^-2

Sequence (Quadratic)

Find the n^th term:

$8, 15, 24, 35, 48, $

$n^2+4n+3$

Standard Form 5

Multiply 7 × 10²
by 9 × 10⁶ and give the answer in standard form.

= 6.3 × 10⁹

Equations (Quadratic 1)

Solve:

$x^2+2x-8= 0$

$x = 2$ and $-4$

Equations (Quadratic 2)

Solve this equation giving the solutions to 3 significant figures:

$3x^2-5x-5 = 0$

$x = 2.37$ and $-0.703$

Polygon Angles

What is the size of each interior angle of a regular hexagon?

120°

Change The Subject

Make $g$ the subject of the formula
$$e=\frac{g}{h}+d$$

$$g=h(e-d)$$

Basic Division 1

Calculate the value of:

864 ÷ 2

= 432

Number Sequences 2

What is the 8th:
a) Cube number; 512
b) Triangular number; 36
c) Fibonacci number. 21

Square Numbers

What is the square root of

100

10

Prime Numbers

What is the 12th prime number?

37

Last Lesson

Write down something you learnt in the previous mathematics lesson.

Last Week

Write down something you learnt in one of the mathematics lessons last week.

Angles

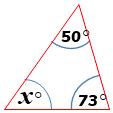
Calculate $x$.

Decimals (Ordering)

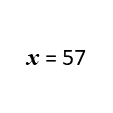
Write down these numbers: 8.8, 8.08, 0.88, 8, 8.88, 0.8, 0.08, in ascending order.
0.08, 0.8, 0.88, 8, 8.08, 8.8, 8.88,

Lengths (Ordering)

Write down these lengths: 1.8m, 17cm, 18mm, 1.08m, 107cm, 1.7cm, in order.
1.7cm, 18mm, 17cm, 107cm, 1.08m, 1.8m,

Capacities (Ordering)

Write down these capacities: 17cl, 173ml, 21cl, 200ml, 18cl, 18ml, in order.
18ml, 17cl, 173ml, 18cl, 200ml, 21cl,

Angles with Parallels 1

Angle diagram d = 99

Angles with Parallels 2

Angle diagram f = 65

Rounding (1sf)

Round to one significant figure:
a) 73.66; 70
b) 162733; 200000
c) 50; 50
d) 0.00407; 0.004

Estimation

Round each value to one significant figure to make an estimate:$$(161 + 8.7) \div 18$$$(200 + 9) \div 20 = 10.45$

Pie Charts (1)

A pie chart shows the colours of 12 books. What sector angle represents the
7 red books?
210°

Graph Linear (2)

What is the equation?

$y=8-2x$

Pie Charts (2)

A pie chart shows the colours of 120 hats. How many green hats are represented
by a sector
angle of 126°?
42